ЗАНЯТИЕ ПЕРВОЕ
КРАТКИЕ СВЕДЕНИЯ О СИСТЕМЕ
ГЕОМЕТРИЧЕСКОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС
Система Симплекс является средой
геометрического моделирования и основана на принципах визуального
проектирования геометрических построений. Система позволяет автоматизировать
рутинные операции, выполняемые человеком при решении геометрических задач.
Любое геометрическое построение, которое можно использовать для решения
какой-либо прикладной задачи, рассматривается как алгоритм, а процесс его
создания с помощью системы Симплекс является программированием.
Начертательная геометрия как наука
изучает алгоритмы, связанные с геометрическими построениями, поэтому для
изучения курса и решения практических задач система Симплекс является наиболее
удобной по сравнению с CAD-системами, предназначенными для производства
технической документации.
Программирование в системе
осуществляется путем установления связей причинно-следственной зависимости
(отношений) между геометрическими объектами. Система оперирует со следующими
геометрическими объектами:
1. Точка (вещественной или
комплексной плоскости). Точка может быть собственной точкой плоскости или
бесконечно-удаленной (несобственной).
2. Прямая линия.
3. Вектор.
4. Окружность.
5. Коника (кривая второго
порядка).
6. Контур.
7. Кривая Безье.
8. Размерные линии.
9. Шкалы.
10. Бинарные поля.
11. Проективные преобразования
(коллинеация, проективитет точечных рядов, проективитет пучков прямых).
12 Размерные линии.
К негеометрическим объектам,
которые также могут быть использованы в системе, относятся:
1. Числовая величина (вещественная
и комплексная).
2. Логическая величина
3. Текст.
Особое место занимает т.н. NIL-объект или объект с
неопределенным значением, который может образовываться в результате
невозможности какой-либо геометрической операции.
В системе также можно
конструировать объекты производных типов, основанных на перечисленных базовых
типах, однако в учебной версии данная возможность отключена.
Любой объект (или совокупность
объектов) обозначается индивидуальным именем. Наличие в системе двух разных
объектов (совокупностей) с одним и тем же именем невозможно. Имя записывается
как последовательность алфавитно-цифровых символов, первый из которых не может
быть числом (например, p1, o2).
Строчные и прописные символы считаются различными. Особо выделены символьные
конструкции:
nil – объект с неопределенным значением
iline –
бесконечно-удаленная прямая
true –
«истинное» значение логической величины
false –
«ложное» значение логической величины.
Эти конструкции нельзя
использовать в качестве имен объектов.
При вызове диалоговых панелей, в
которых задаются параметры отношений, система предлагает именовать объекты в
соответствии со следующим правилом: первый символ имени соответствует типу
объекта, создаваемого в конкретном выходном параметре, а за ним следует число,
предлагаемое системой. Соответствие типов и символов для имен следующее:
Числовые величины – c.
Точки – p.
Прямые линии – o.
Векторы – v.
Окружности – d.
Коники – y.
Контуры – w.
Кривые Безье – z.
Логические величины – g.
Размерные линии – f.
Шкалы – h.
Бинарные поля – b.
Текстовые последовательности – t.
Проективные преобразования
(коллинеация, проективитет точечных рядов, проективитет пучков прямых) – k, r, l.
Объекты вводятся в систему как
входные и выходные параметры отношений. Каждое отношение может рассматриваться
как элементарный преобразователь с неизвестной внутренней структурой (черный
ящик) на вход которого подаются геометрические сигналы (объекты-предки), а на
выходе возникают другие геометрические сигналы (объекты-потомки), зависящие как
от входных объектов, так и от конкретного вида отношений. В системе Симплекс
около 150 стандартных отношений, которые могут быть использованы при решении
конкретных задач.
Познакомимся с внешним видом
рабочего поля системы и основными приемами работы.
Экран системы подразделяется на
следующие области:
|
Рисунок 1 |
1. Главное меню системы.
2. Кнопки чтения и записи проекта
на носители информации.
3. Кнопки операций с буфером
временного хранения Clipboard.
4. Вызов наиболее употребительных
отношений.
5. Кнопки переключения палитр
отношений. На кнопках условно обозначены типы выходных объектов, создаваемых
группами отношений.
6. Кнопки вызова отношений.
7. Окно реализации геометрического
алгоритма.
8
Статусная строка.
9 Кнопки переключения режима
курсора.
Для того чтобы начать
геометрическое построение необходимо загрузить систему в оперативную память ЭВМ
(например, двойным щелчком мыши над иконкой ![]() ), после чего в ответ на запрос фамилии и инициалов автора
проекта ввести необходимые сведения. Они необходимы для координации действий студентов
и преподавателя в условиях дистанционного обучения. В Симплексе любые
построения представляют собой проект, который, в свою очередь, подразделяется
на один или несколько алгоритмов. Для того чтобы создать новый проект,
необходимо в меню Файл выбрать пункт Новый проект.
При этом откроется окно реализации алгоритма (7) и алгоритму присвоится имя Главный.
), после чего в ответ на запрос фамилии и инициалов автора
проекта ввести необходимые сведения. Они необходимы для координации действий студентов
и преподавателя в условиях дистанционного обучения. В Симплексе любые
построения представляют собой проект, который, в свою очередь, подразделяется
на один или несколько алгоритмов. Для того чтобы создать новый проект,
необходимо в меню Файл выбрать пункт Новый проект.
При этом откроется окно реализации алгоритма (7) и алгоритму присвоится имя Главный.
По окончании работы проект следует
сохранять (пункты Файл/Сохранить как), при этом исходное имя
проекта Untitled можно (и следует!) указать в имени сохраняемого
файла. Проекты Симплекса хранятся на носителях информации в файлах с
расширением SPX.
Рассмотрим подробнее средства
управления окном реализации алгоритма (7).
|
Рисунок 2 |
10. Область геометрических
построений.
11. Кнопки управления масштабом
изображения (увеличить, уменьшить, сделать равным единице).
12. Закладки переключения
координатных систем (обычная геометрия, комплексная геометрия).
13. Закладки переключения слоев.
Обычно построения ведутся в слое основной. При необходимости
исключить из изображения какие-либо объекты, их следует перенести в другой
слой, для чего его нужно создать. Способ создания слоя будет рассмотрен ниже.
Слой all позволяет отобразить в области геометрических построений
объекты, относящиеся ко всем слоям.
14. Смещение области
геометрических построений.
Попробуем выполнить элементарные
геометрические построения, например, построить точку с координатами X=10, Y=10.
Для этого в палитре 6 следует
нажать на кнопку ![]() . На экране появится панель описания отношения
Точка задана двумя координатами.
. На экране появится панель описания отношения
Точка задана двумя координатами.
|
Рисунок 3 |
(То же самое можно было бы
сделать, вызвав панель описания отношения из главного меню Отношения/Точка/Координатами).
Рассмотрим подробнее структуру
панели описания отношения.
|
Рисунок 4 |
Числом 15 обозначено поле задания
имен выходных параметров. В других отношениях количество таких полей может быть
разным. Если описывается новое отношение, то система автоматически заполняет поля
выходных параметров новыми именами. Если же требуется изменить уже имеющееся в
алгоритме отношение, то в эти поля вписываются имена объектов, которые были
объявлены таким отношением ранее. Имена объектов и названия выходных параметров
изображены коричневым цветом.
Числом 16 обозначена область
задания имен выходных параметров отношения. Количество полей во входных
параметрах отношений также может быть различным. Поля должны быть заполнены
именами объектов или константами. Это
можно сделать, либо набирая текст с клавиатуры компьютера, либо указывая
курсором (стрелкой) на объекты, изображенные в области геометрических
построений (в этом случае система определяет имена указанных объектов и
автоматически подставляет их во входные поля). Имена объектов и названия
входных параметров изображены синим цветом.
Если все поля отношения заполнены
синтаксически правильными конструкциями, то активизируются кнопки Тест
(20) и Ввод (19). Они предназначены для включения отношения в
состав алгоритма. Система занесет отношение в алгоритм, исследует, какие
изменения произошли в алгоритме в результате появления нового отношения,
сделает расчет, отобразит новое состояние построения и перейдет в режим
ожидания нового отношения. Разница между кнопками состоит в том, что при нажатии
на кнопку Ввод в полях 15 будут подготовлены имена для нового
отношения. При нажатии на кнопку Тест система оставит содержимое
полей без изменения. Такой режим ввода отношений полезен, если у разработчика
нет полной уверенности в корректности задания входных параметров, и ему
требуется проверка его предположений без изменения вида введенной информации.
Назначение полей 17, 18 и 21 будет
объяснено в следующих занятиях.
Итак, в появившуюся панель занесем
следующее:
1. в поле параметра X число 10.
2. в поле параметра Y число 10.
3. нажмем кнопку Ввод.
В окне реализации алгоритма
появится точка
|
Рисунок 5 |
Рисунок 6 |
Для того чтобы надписать имена объектов
возле их изображений, следует нажать клавишу F5, вызывающую панель включения меток объектов и меток
ориентации линий.
|
Рисунок 7 |
Отметим те типы объектов (точка),
для которых система должна надписывать, метки и нажмем Ввод.
|
Рисунок 8 |
Рисунок 9 |
Полученная точка называется
свободной, потому что задана координатами, выраженными числовыми константами.
Такую точку можно переместить в любое место, если перевести систему в режим
динамического редактирования положений объектов (точек), нажав кнопку ![]() (9). Курсор
(9). Курсор ![]() в окне реализации
алгоритма изменит вид на
в окне реализации
алгоритма изменит вид на ![]() (шейпер). Далее следует выполнить следующие действия:
(шейпер). Далее следует выполнить следующие действия:
1. Поместить острие шейпера над
изображением точки p1.
2. Нажать левую кнопку мыши.
3. Не отпуская кнопку передвинуть
шейпер в новое положение.
4. Отпустить кнопку.
Зацепляя шейпером свободную точку,
можно отбуксировать ее в любое положение (действия с мышью похожи на технологию
drag and drop, типичную для среды Windows). Следует не забывать после
завершения работы в режиме динамического редактирования возвращать курсор в
режим указателя, нажимая для этого кнопку ![]() .
.
|
В начале буксировки |
В конце буксировки |
|
Рисунок 10 |
Рисунок 11 |
Свободную точку можно ввести в
алгоритм, указывая ее положение в области геометрических построений мышью. Для
этого необходимо нажать на кнопку ![]() и центром перекрестия
появившегося курсора
и центром перекрестия
появившегося курсора ![]() указать положение
точки. Поля панели ввода отношения заполнятся
автоматически.
указать положение
точки. Поля панели ввода отношения заполнятся
автоматически.
|
Рисунок 12 |
Рисунок 13 |
Теперь между точками p1 и p2 проведем
прямую линию. Переключим палитру инструментов 6 на отображение кнопок для
вызова отношений, порождающих прямые линии. Для этого нажмем на кнопку ![]() (5), изменяющую
состав палитры 6:
(5), изменяющую
состав палитры 6:  и нажмем на
кнопку
и нажмем на
кнопку ![]() . В результате этих действий будет вызвана панель описания
отношения Прямая задана двумя точками.
. В результате этих действий будет вызвана панель описания
отношения Прямая задана двумя точками.
|
Рисунок 14 |
Подведем курсор-указатель ![]() к
изображению точки p1 и нажмем
левую кнопку мыши. Имя точки окажется в поле входного параметра Точка 1.
к
изображению точки p1 и нажмем
левую кнопку мыши. Имя точки окажется в поле входного параметра Точка 1.
|
Рисунок 15 |
Рисунок 16 |
Теперь подведем курсор к
изображению точки p2 и нажмем
левую кнопку мыши. Имя точки окажется в поле входного параметра Точка 2.
Активизируются кнопки Тест и Ввод.
|
Рисунок 17 |
Рисунок 18 |
Нажав кнопку Ввод,
получим следующее изображение:
|
Рисунок 19 |
Попробуем изменять точку p1, выполняя
динамическое редактирование ее положение с помощью шейпера ![]() . Важно заметить, что при любых изменениях положения точки p1
изменяется и отрезок прямой o1, так как
он является потомком измененной точки p1.
. Важно заметить, что при любых изменениях положения точки p1
изменяется и отрезок прямой o1, так как
он является потомком измененной точки p1.
|
Рисунок 20 |
Рисунок 21 |
Проследить зависимость объектов в
алгоритме, если с помощью клавиши F6 вызвать
окно структуры алгоритма.
|
Рисунок 22 |
Здесь прямоугольники с
пиктограммами, соответствующими кнопкам вызова отношений, обозначают отношения,
составляющие алгоритм. Объекты изображены линиями, связывающими отношения.
Объекты, надписанные слева от отношения, являются его входными параметрами, а
справа – выходными. Изменяясь по каким-либо причинам, объекты влияют на
отношения, для которых они являются входными параметрами. В свою очередь такие
отношения активизируются и изменяют значения своих выходных объектов. Таким
образом, процесс расчета алгоритма осуществляется до тех пор, пока не завершится
перерасчет значений всех объектов-потомков объекта, вызвавшего изменение
алгоритма.
Анализ структуры алгоритма позволяет
понять различия в способах операции удаления объектов (команда меню Редакция/Изъять).
(Команда Изъять переносит отношения из алгоритма в Clipboard).
Прежде всего, следует заметить, что
удаляются не объекты, а порождающие их отношения. Это значит, что в результате
удаления отношения потеряют значения все выходные параметры этого отношения (их
может быть несколько), а также потомки объектов, определяемых удаленным
отношением.
Например, удалим отношение,
объявляющее точку p1. Для этого убедимся, что на экране нет панели
описания отношения (если она есть, то ее надо закрыть), выделим точку p1,
указав на нее курсором ![]() .
.
|
Рисунок 23 |
Вызовем команду основного меню Редакция/Изъять.
(Аналогичная команда имеется во всплывающем меню окна реализации алгоритма). В
появившемся окне следует указать способ удаления (с предками, с потомками,
только отношение). Выберем кнопку Изъять только отношение.
|
Рисунок 24 |
Снова обратимся к окну структуры
алгоритма. Как видно из него, теперь алгоритм не содержит отношение,
определяющее p1, однако
отношение, определяющее потерявшее значение (красная линия в окне структуры) и
отображение прямую о1, ссылается на p1 как на вакантный объект. Как только в алгоритме
появится новое отношение, объявляющее точку p1, будет рассчитано новое значение o1.
|
Рисунок 25 |
Введем отношение Точка задана
координатами для объявления точки p1, заполним поля и нажмем Ввод.
|
Рисунок 26 |
Рисунок 27 |
|
Рисунок 28 |
Закроем панель отношения.
Предположим теперь, что необходимо
изменить значения координат в отношении для точки p1.
Выделим точку p1 и вызовем
пункт Редактировать всплывающего меню окна реализации алгоритма.
Появится панель, заполненная параметрами отношения для объявления точки p1.
|
Рисунок 29 |
Рисунок 30 |
Введем новые значения и нажмем
кнопку Ввод.
|
Рисунок 31 |
В этот раз система обнаружит
противоречие нового отношения, объявляющего p1 с отношением для p1, уже объявленном в алгоритме. Пользователь должен
решить, заменить ли имеющееся отношение новым, или же он ошибочно сформировал
новое отношение, и ему следует отказаться от замены.
|
Рисунок 32 |
В случае ошибочного ввода
отношения Симплекс позволяет вернуться на один шаг программирования назад. Это
можно сделать если выбрать пункт основного меню Редакция/Восстановить,
либо нажать на кнопку ![]() .
.
Выбирая пункт меню Протокол/Программы,
пользователь может получить полный перечень отношений, составляющих алгоритм.
Важно заметить, что особенностью Симплекса как среды программирования, является
отсутствие требований к порядку ввода отношений в алгоритм. Поэтому в отличие от
многих других недекларативных языков программирования при решении задач в
Симплексе нет необходимости указывать относительное положение отношения среди
других как строки программы.
|
Рисунок 33 |
Выбирая пункт меню Протокол/Значений объектов,
можно получить числовые эквиваленты объектов, участвующих в алгоритме.
|
Рисунок 34 |
Следует также указать на
возможность перехвата изображения окна реализации алгоритма командой главного
меню Окно/Копирование окна.
Выполняя данную команду, Симплекс помещает Bitmap-изображение активного окна реализации алгоритма в Clipboard, откуда оно может быть помещено в
любые приложения Windows,
обрабатывающие Bitmap-изображения.
Этой возможностью можно пользоваться для оперативного взаимодействия с
преподавателем, пересылая изображение, пометки на нем и текстовые комментарии
по электронной почте. Однако окончательным подтверждением правильности
полученных результатов является файл проекта с алгоритмом, который является
основанием для зачета представленной на проверку работы.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание
Выполнить построение чертежа, изображенного на рис. 35, с
помощью системы Симплекс.
Учебная цель:
Знакомство с функциональным составом системы и освоение
приемов работы.
|
|
Рисунок 35
Построить чертеж детали, изображенной на рис. 1 с применением системы Симплекс.
Загрузим систему Симплекс в оперативную
память вычислительной машины ![]() . После загрузки на
экране образуется главное окно системы:
. После загрузки на
экране образуется главное окно системы:
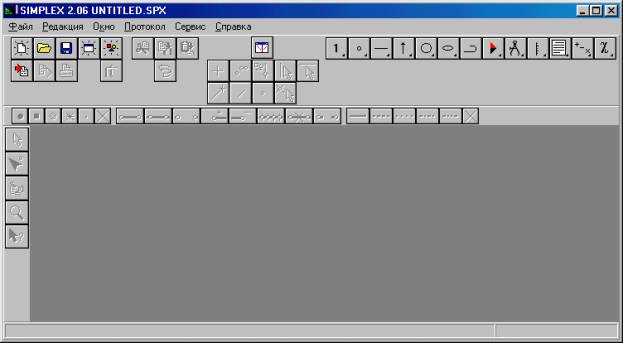
Рисунок 36
Создадим новый проект, выбрав
пункты меню Файл / Новый проект. При этом откроется окно реализации
геометрического алгоритма:
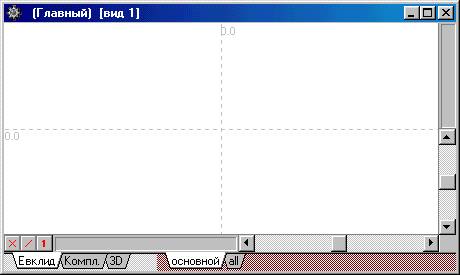
Рисунок 37
Все построения чертежа будем выполнять, используя функции системы Симплекс в этом окне. Перед тем как начать построение чертежа создадим дополнительный слой, на который будем помещать вспомогательные графические объекты. Для этого выведем курсор в белую область окна реализации алгоритма и нажмем правую кнопку мыши, в результате чего на экране образуется всплывающее меню:
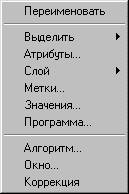
Рисунок 38
Выберем пункт Слой и подпункт Добавить:
![]() .
.
Рисунок 39
В появившейся диалоговой панели
система предлагает образовать новый слой с названием слой1. Нажмем
кнопку Ввод для подтверждения.
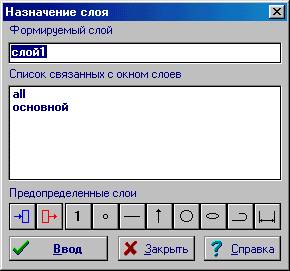
Рисунок 40
Теперь среди закладок слоев в окне
реализации алгоритма имеется закладка, указывающая на слой слой1.
Начнем построения.
|
Исходное состояние
алгоритма. |
Рисунок 41 |
Прежде всего, необходимо ввести некоторую точку,
относительно которой будут выполняться все остальные построения. Пусть это
будет точка p1 с
координатами X=0 и Y=0. Для
указания этой точки вызовем функцию Точка задана координатами.
|
Рисунок 42 Точка <p1>
задана координатами <0> и <0>. |
Рисунок 43 |
Для того чтобы быстро и эффективно строить чертеж необходимо
ввести вспомогательные геометрические объекты - оси. На нашем чертеже таких
осей четыре. Через точку p1 проходят
одна горизонтальная и одна вертикальная оси. Построим их, вызвав функцию Прямая,
проходящая через точку под углом к оси OX.
|
Рисунок 44 Прямая <o1>
задана точкой <p1> и
углом <0> к оси OX. |
Рисунок 45 |
|
Рисунок 46 Прямая <o2>
задана точкой <p1> и
углом <90> к оси OX. |
Рисунок 47 |
Оставшиеся две горизонтальные оси
целесообразно построить в соответствии с указанными в задании размерами,
воспользовавшись функцией Прямая, параллельная прямой.
|
Рисунок 48 Прямая <o3> проведена
параллельно прямой <o1> на расстоянии <84>. |
Рисунок 49 |
|
Рисунок 50 Прямая <o4>
проведена параллельно прямой <o3> на расстоянии <60>. |
Рисунок 51 |
Особый характер этих прямых
обязывает выполнять их изображение специальным начертанием – штрих-пунктирной
линией. В Симплексе будет удобнее отличать эти линии от других, если поменять
стиль полученных линий со сплошного на штрих-пунктирный. Для этого, удерживая
на клавиатуре клавишу Shift,
указателем мыши последовательно отметим изображения линий. При этом в окне
реализации алгоритма выделенные линии временно изменят свою толщину.
|
|
Рисунок 52 |
По окончании выделения, следует
поместить курсор мыши над световой кнопкой стиля штрих-пунктирной линии ![]() и нажать левую кнопку
мыши. Следует заметить, что поскольку система изменяет атрибуты совокупности
объектов, на экран монитора выводится диалоговая панель, требующая уточнения,
каким именно объектам следует изменить атрибут. В нашей задаче следует изменить
атрибуты всех линий, следовательно, в диалоговой панели надо нажать на кнопку Ко
всем. Результат изменения атрибутов представлен на рис. 54.
и нажать левую кнопку
мыши. Следует заметить, что поскольку система изменяет атрибуты совокупности
объектов, на экран монитора выводится диалоговая панель, требующая уточнения,
каким именно объектам следует изменить атрибут. В нашей задаче следует изменить
атрибуты всех линий, следовательно, в диалоговой панели надо нажать на кнопку Ко
всем. Результат изменения атрибутов представлен на рис. 54.
|
Рисунок 53 |
Рисунок 54 |
Теперь можно построить окружности
около центра p1. В
задании указаны диаметры этих окружностей, поэтому для их ввода в алгоритм целесообразно
воспользоваться функцией Окружность задана центром и диаметром.
|
Рисунок 55 Окружность <d1>
задана центром <p1> и диаметром <15>. |
Рисунок 56 |
|
Рисунок 57 Окружность <d2>
задана центром <p1> и диаметром <30>. |
Рисунок 58 |
Центры остальных окружностей пока не известны. Их можно построить, найдя точки пересечения осей.
|
Рисунок 59 Точка <p2> есть
пересечение прямых <o2> и
<o3>. |
Рисунок 60 |
|
Рисунок 61 Точка <p3>
есть пересечение прямых <o2> и
<o4>. |
Рисунок 62 |
Строим оставшиеся четыре окружности.
|
Рисунок 63 Окружность <d3>
задана центром <p2> и диаметром <25>. |
Рисунок 64 |
|
Рисунок 65 Окружность <d4>
задана центром <p2> и диаметром <55>. |
Рисунок 66 |
|
Рисунок 67 Окружность <d5>
задана центром <p3> и диаметром <10>. |
Рисунок 68 |
|
Рисунок 69 Окружность <d6> задана
центром <p3> и диаметром <24>. |
Рисунок 70 |
Ребро жесткости представленной в
задании детали следует построить, применяя функцию Прямая, параллельная
прямой, в соответствии с указанными размерами.
|
Рисунок 71 Прямая <o5>
проведена параллельно прямой <o2> на расстоянии <-4>. |
Рисунок 72 |
|
Рисунок 73 Прямая <o6>
проведена параллельно прямой <o2> на расстоянии <4>. |
Рисунок 74 |
Заметим, что мы получили
бесконечные линии o5 и o6. Они
будут играть роль вспомогательных линий, необходимых для выполнения сопряжений
радиусом 5 мм.
Размер 42 мм указывает положение двух
точек, необходимых для построения прямых линий, касательных к окружности d2. Построим
эти точки, применяя функцию Точка относительно точки по приращениям.
|
Рисунок 75 Точка <p4>
задана относительно точки <p2> с приращениями по X <21> и Y <0>. |
Рисунок 76 |
|
Рисунок 77 Точка <p5>
задана относительно точки <p2> с приращениями по X <-21> и Y <0>. |
Рисунок 78 |
Проведем правую касательную.
Функция Касание прямой к окружности позволяет задать не только
касательную, но и определить точку касания прямой и окружности.
|
Рисунок 79 Точка касания <p6>
на окружности <d2> и касательная <o7> из точки <p4>. |
Рисунок 80 |
Попробуем построить левую
касательную. Но в отличие от предыдущей диалоговой панели нажмем кнопку Тест.
|
Рисунок 81 Точка касания <p7> на
окружности <d2> и касательная <o8> из
точки <p5>. |
Рисунок 82 |
Обратим внимание на то, что
образовалась не так касательная, которая ожидалась. Это связано с тем, что результат
зависит от ориентации окружности. В нашем случае окружность ориентирована
против часовой стрелки (т.к. ее диаметр задан положительным числом). Двигаясь от исходной точки p4 по
касательной o7, мы плавно
переходим на окружность в направлении ее ориентации. Для того чтобы построить
«правильную» касательную, необходимо в параметрах функции указать
противоположную ориентацию окружности, для чего поставить перед ее именем знак
минус. Поскольку была нажата кнопка Тест, содержание полей панели
не изменилось, и сделать нужное исправление просто. Если же все-таки была
нажата кнопка Ввод, то для исправления построения надо сделать
следующее:
1. Закрыть диалоговую панель.
2. В окне реализации алгоритма выделить курсором объект, подлежащий исправлению.
3. Нажать правую кнопку мыши для
вызова всплывающего меню.
4. Выбрать пункт Редактировать.
В результате выполненных действий
будет вызвана диалоговая панель, отвечающая за назначение корректируемого
объекта.
|
Рисунок 83 Точка касания <p7> на
окружности <-d2> и касательная <o8> из
точки <p5>.
Рисунок 84 |
Рисунок 85 |
Для чертежа необходимы лишь части
от образованных касательных. Применяя функцию Точка пересечения прямой и
окружности, найдем точки, ограничивающие касательные o7 и o8.
|
Рисунок 86 Точки <p8> и
<p9> есть пересечение прямой <o7> и
окружности <d4>. |
Рисунок 87 |
|
Рисунок 88 Точки <p10> и
<p11> есть пересечение прямой <o8> и
окружности <d4>. |
Рисунок 89 |
Теперь касательные в том виде, в
котором они имеются на нашем чертеже, не нужны. Удалять касательные o7 и o8 из
алгоритма ни в коем случае нельзя, так как при этом будет потеряна информация о
причинно-следственной взаимосвязи объектов, зависящих от o7 и o8 (такими
объектами, например, являются точки p8, p9, p10 и p11).
Прямые o7 и o8 следует
перенести на вспомогательный слой слой1, чтобы они не были видны в слое основной.
Для этого выделяем с нажатой клавишей Shift объекты o7 и o8 и, не
отпуская левой кнопки мыши после выделения последнего объекта, перетаскиваем
курсор на изображение закладки слоя слой1. Таким образом, мы выполним
изменение атрибута слоя касательных.
|
Рисунок 90
Рисунок 91 |
Рисунок 92 |
Используя точки p6, p8, p7 и p10
достраиваем необходимые элементы чертежа.
|
Рисунок 93 Прямая <o9>
задана точками <p6> и
<p8>. |
Рисунок 94 |
|
Рисунок 95 Прямая <o10>
задана точками <p7> и
<p10>. |
Рисунок 96 |
Теперь приступим к построению сопряжений.
Выполним сопряжение прямой o6 с окружностью d2 радиусом 5 мм, для чего вызовем функцию Окружность
касательно к окружности и прямой.
|
Рисунок 97 Окружности <d7> и
<d8> радиуса <5> касаются окружности
<d2> и прямой <o6> в
точках <p12> и
<p13>, <p14> и
<p15>. |
Рисунок 98 |
Отметим, что прямая o6 визуально
укоротилась. Это происходит из-за того, что на ней, изначально заданной бесконечной
прямой, образовались две принадлежащие ей точки. Такие точки называют точками,
инцидентными прямой. Укорочение прямой позволяет уменьшить интенсивность
заполнения чертежа линиями, но в то же время прямая остается неограниченной и
может взаимодействовать с другими объектами как бесконечная.
|
Рисунок 99 Окружности <d9> и
<d10> радиуса <5> касаются окружности
<d4> и прямой <o6> в
точках <p16> и
<p17>, <p18> и
<p19>. |
Рисунок 100 |
Построение сопряжений на прямой o5 без учета
ориентации прямой и окружности может привести к следующему результату:
|
Рисунок 101 Окружности <d11>
и <d12> радиуса <5> касаются окружности <d2>
и прямой <o5> в точках
<p20> и <p21>, <p22> и <p23>. |
Рисунок 102 |
При указании положительной ориентации прямой в параметрах функций, выполняющих сопряжения, сопрягающая окружность будет образована с правой стороны от ориентированной прямой, в противном случае с левой. При указании положительной ориентации исходной окружности сопрягающая окружность строится вне исходной, в противном случае внутри.
|
Рисунок 103
Рисунок 104 Окружности <d11> и
<d12> радиуса <5> касаются окружности
<d2> и прямой <-o5> в
точках <p20> и
<p21>, <p22> и
<p23>. |
Рисунок 105 |
Теперь сопрягающая окружность
построена правильно, но сопрягающая дуга противоположна той, которая требуется.
Установить правильный тип дуги можно, если изменить атрибут ее типа на тип
«внешняя линия». Для этого необходимо выделить дуги и нажать на кнопку ![]() .
.
|
Рисунок 106
Рисунок 107 |
Рисунок 108 |
Аналогично строим сопряжения прямой o5 с
окружностью d4.
|
Рисунок 109 Окружности <d13> и
<d14> радиуса <5> касаются окружности
<d4> и прямой <-o5> в
точках <p24> и
<p25>, <p26> и
<p27>. |
Рисунок 110 |
|
Рисунок 111
Рисунок 112 |
Рисунок 113 |
Изображения «лишних»
объектов переместим на слой слой1.
|
Рисунок 114
Рисунок 115 |
Рисунок 116 |
Достраиваем вертикальные линии ребра жесткости.
|
Рисунок 117 Прямая <o11>
задана точками <p15> и
<p16>. |
Рисунок 118 |
|
Рисунок 119 Прямая <o12>
задана точками <p23> и
<p24>. |
Рисунок 120 |
Сопряжение окружностей d4 и d6 радиусом 18
мм выполняем с помощью функции Окружность, касательная к двум окружностям.
Окружность-результат будет построена со внешней стороны исходной окружности,
указанной с положительной ориентацией. В противном случае – с внутренней.
|
Рисунок 121 Окружности <d15> и
<d16> радиуса <18> касаются окружностей
<d4> и <d6> в
точках <p28> и
<p29>, <p30> и
<p31>. |
Рисунок 122 |
|
Рисунок 123 |
Рисунок 124 |
Из приведенного правила есть одно
исключение. Оно касается случая, когда сопрягающая окружность сама охватывает
обе исходные. Возможные варианты представлены ниже.
|
Рисунок 125 Окружности <d17> и
<d18> радиуса <64> касаются окружностей
<d4> и <d6> в
точках <p32> и
<p33>, <p34> и
<p35>. |
Рисунок 126 |
|
Рисунок 127 |
Рисунок 128 |
|
Рисунок 129 |
Рисунок 130 |
|
Рисунок 131 Окружности <d17> и
<d18> радиуса <64> касаются окружностей
<-d4> и <-d6> в
точках <p32> и
<p33>, <p34> и
<p35>. |
Рисунок 132 |
|
Рисунок 133 |
Рисунок 134 |
Чертеж построен. Остается лишь
привести в «аккуратный» вид изображения осевых линий, для чего их следует
пересечь с окружностями.
|
Рисунок 135 Точки <p36> и
<p37> есть пересечение прямой <o2> и
окружности <d2>. |
Рисунок 136 |
|
Рисунок 137 Точки <p38> и
<p39> есть пересечение прямой <o1> и
окружности <d2>. |
Рисунок 138 |
|
Рисунок 139 Точки <p40> и
<p41> есть пересечение прямой <o3> и
окружности <d4>. |
Рисунок 140 |
|
Рисунок 141 Точки <p42> и
<p43> есть пересечение прямой <o4> и
окружности <d6>. |
Рисунок 142 |
|
Рисунок 143 Точки <p44> и
<p45> есть пересечение прямой <o2> и
окружности <d6>. |
Рисунок 144 |
Изображения точек больше не нужны.
Для того чтобы быстро выделить все точки создадим слой точек.
|
Рисунок 145 |
Рисунок 146 |
Выделим все объекты, которые видны
в слое, для чего во всплывающем меню окна реализации алгоритма выберем пункты Выделить
/ Все видимое в слое и перенести выделение в слой1.
|
Рисунок 147 |
Рисунок 148 |
Слой слой1 является
хранилищем всех вспомогательных объектов.
|
Рисунок 149 |
|
Окончательный вид чертежа. Проект можно сохранить на диске.
|
Рисунок 150 |
|
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Повторить построение чертежа,
рассмотренного в данном руководстве.
2. Выполнить один вариант
высланного чертежа, сохранить проект и прислать на проверку (файлы с
расширением SPX и PRT). Файлы можно архивировать. При возникновении
вопросов к письму следует приложить файлы SPX и PRT.
Замечания:
1. Если на чертеже следует
построить дугу окружности, то сначала строится сама окружность, а затем с
помощью функции Дуга на окружности строится дуга по исходной
окружности, начальной и конечной точкам дуги. Исходная окружность переносится
на служебный слой.
2. Перенос объекта со служебного
слоя в основной, если это необходимо, выполняется аналогично переносу объекта
из основного слоя в служебный.
3. Особенно внимательно следует
относиться к операции удаления объектов. Нерациональное удаление объекта вместе
с его предками может привести к потере чертежа.
4. Размерные линии можно не
изображать.














































































































































